رشد تصاعدی و ویروس کرونا
جملههایی چون «کرونا بیخطرتر از تبلیغات آن است» یا «همه ما ویروس آنفلوآنزا را تجربه کردهایم، پس بزرگنمایی نکنیم» را از افراد و چه بسا پزشکان میشنویم. اما سوال اینجاست که آیا این ویروس نوظهور واقعا بیخطرتر از شهرتش است؟ پاسخ به این سوال منفی است. چرا که این ویروس نه تنها رشد تصاعدی بلکه ضریب ابتلای به مراتب بالاتر از ویروس آنفلولانزا دارد.
قدرت هر ویروس با شاخص ضریب ابتلای آن (basic reproductive number) سنجیده میشود. این شاخص نشان میدهد هر ویروس به طور متوسط چند فرد را آلوده میکند. آنفلوانزای اسپانیایی در سال ۱۹۱۸ و سپس ۱۹۲۰ با ضریب ابتلای ۱٫۸ نفر توانست حدود ۵۰ میلیون قربانی در جهان بگیرد. در مورد کرونا این عدد مطابق دادههای سازمان بهداشت جهانی مابین ۲ تا ۳٫۱ است. یعنی هر فرد مبتلا به طور متوسط ۲ تا ۳٫۱ نفر دیگر را هم آلوده میکند. این شاخصها «موتورِ تصاعد» را در یک سیر پیشرونده روشن میکند.
فرآیندهای رشد در طبیعت معمولا روندی خطی دارند. کودکان، گیاهان و اکثر موجودات زنده اطراف ما رشدی خطی دارند و مثلاً سالی x مقدار رشد میکنند. تنها معدود فرایندهای طبیعی همچون انفجار اتمی، رشد مولکولهای مخمر نان و یا تکثیر ویروسها را میتوان مثال زد که رشدی تصاعدی داشته باشند و در مدت زمان مشخصی دوبرابر شوند. معادله تصاعدی رشد آنها و سرعت اعجابانگیز این نوع رشد باعث میشود که ذهن بشر از درک آن ناتوان شود.
درماندگی ذهن در مقابل اعداد بزرگ
اعداد بزرگ محدودیت ادراک ذهن افراد را آشکار می کنند. ذهن ما مفهوم رشد تصاعدی را نمیفهمد. ما فقط رشد خطی را درک میکنیم. اگر بخواهیم چند کلمه حرف «حساب» بزنیم باید به پایهایترین علم یعنی ریاضی برگردیم.
ذهن ما فقط توانایی جمع، آن هم جمع دو عدد را دارد. بعید است کسی باشد که بتواند سه عدد را همزمان با هم جمع کند. منظور فقط عددهای بزرگ نیست. در مورد عددهای کوچک هم همینطور است. مثلاً اگر شما بخواهید عددهای ۵ و ۸ و ۹ را با هم جمع کنید، فقط میتوانید دو تا از آنها را با هم جمع بزنید و در مرحلهی بعدی حاصل آنها را با عدد سوم جمع بزنید. وقتی از جمع یک قدم فراتر برویم به ضرب میرسیم. ضرب اصلا وجود خارجی ندارد. ضرب چیزی جز جمع مکرر نیست. ذهن ما که توانایی جمع بیش از دو عدد را ندارد، قطعا در انجام عمل ضرب ناتوان است.
به عنوان مثال وقتی میخواهیم حاصل ضرب هفت در ۹ را بدانیم یعنی هفت بار عدد ۹ را جمع بزنیم. همه ما در دوران دبستان حاصل این جمعهای مکرر را از بر کردهایم. هیچ راهی غیر از حفظ کردن نداشتهایم. حالا بیایید یک قدم از ضرب فراتر برویم و به «توان» برسیم. این دیگر از تصور ذهن خارج است. ما مفهوم ضرب را هم به سختی درک میکنیم چه برسد به مفهوم توان. فرض کنید کارفرمایی به کارمندش بگوید برای دستمزدت من روز اول به تو دو تومان میدهم، روز دوم چهار تومان میدهم، روز سوم هشت تومان، روز چهارم ۱۶ تومان و به همین شکل اگر از عملکردت راضی بودم هر روز عدد دستمزدت را دو برابر روز قبل افزایش میدهم.
فکر میکنید اگر این پیشنهاد را به یک کارمند بدهید چقدر احتمال دارد که با آن موافقت کند؟ به احتمال زیاد این پیشنهاد توسط کارمند رد خواهد شد. حالا بیایید حساب کنیم که این عدد در یک ماه چقدر میشود. در روز دهم ۲ به توان ۱۰ میشود ۱۰۲۴، برای راحتی شمارش عدد ۱۰۰۰ را در نظر میگیریم. برای محاسبه این عدد در روز بیستم حاصل آن هزار در هزار یعنی یک میلیون تومان میشود و در روز سیام حاصل آن یک میلیون در هزار یعنی یک میلیارد تومان میشود.
افسانه معروف هندی
افسانه معروفی وجود دارد که آن را به مخترع شطرنج، راهبی هندی به نام وودی رابپ نسبت میدهند. شهرام، پادشاه وقت هندوستان که از اختراع او خوشش آمده از او میپرسد که در مقابل این ابداع چه پاداشی میخواهی؟ مخترع پیر زیرکانه پاسخ میدهد: «ای پادشاه در خانه اول صفحه شطرنج دو دانه گندم قرار بده و خانه به خانه برایم دو برابر کن». پادشاه هند میگوید: «چرا چیز بیشتری از ما طلب نکردی؟» مخترع شطرنج هم میگوید: «من به همین هدیه کوچک قانع هستم.» نکتهای که پادشاه و اطرافیانش از درک آن ناتوان بودند، حجم کلان عدد ۲ به توان ۶۴ دانه گندم بود.
حالا بیایید حساب کنیم در این رشد تصاعدی برای گندمها چه اتفاقی میافتد. عدد خانه دهم شطرنج ۱۰۰۰ میشود، خانه بیستم، یک میلیون، خانه سیام، یک میلیارد، خانه چهلم، هزار میلیارد، خانه پنجاهم یک میلیون میلیارد، خانه شصتم عددی میشود که با یک و هیجده صفر جلوی آن مشخص میشود. تازه باید تمام گندمهای تک تک این خانهها با هم جمع شوند.
حالا در نظر بگیرید وزن هر دانه گندم حدود ۴۰ میلیگرم است. با یک محاسبه ساده وزن گندمهایی که در خانه شصتم شطرنج قرار میگیرد ۴۰ میلیارد تن میشود.
هدف این میزگرد و این یادداشت این است که مسوولان وزارت بهداشت که به آمار دقیق این تختها دسترسی دارند، برنامهریزیهای کلان خود را بر اساس تعداد تختهای ICU انجام بدهند.
برای نشان دادن بزرگی این عدد به گزارش روزنامهی دنیای اقتصاد ۲۵ اسفند ۹۸ دقت کنید که میگوید کل تولید جهانی غلات (نه فقط گندم) در سال ۲۰۱۷، معادل ۲٫۶ میلیارد تن بودهاست. نکتهی قابل تامل در این افسانه این است که پادشاه نتوانست سیر تصاعدی گندمها را ببیند. گویی این داستان تکراری در تاریخ است که نخبهها سیر تصاعدی را میبینند، اما دولتمردان از دیدن آن ناتوان هستند و تصمیمات کلان را بر اساس رشد خطی میگیرند.
درک این مثال ساده به شناخت مدل تکثیر ویروسها کمک میکند. دقیقا همین اتفاق در اپیدمی ویروسی میافتد. رشد تصاعدی در زمان کوتاهی به عددهای عجیب و غریبی منتهی میشود. به همین دلیل است که صدر اعظم آلمان پیشبینی کرده که ۷۰ درصد جمعیت آلمان به این ویروس مبتلا میشوند.
ممکن است تصور شود مثلاً ابتلای هزار نفر در کشور ۸۰ میلیونی ایران که عدد بزرگی نیست! علت این تخمینِ اشتباه این است که ذهن فقط رشد خطی را درک میکند و رشد تصاعدی را نمیفهمد. این یک خطای شناختی است که به آن exponential growth bias گفته میشود.
نگاهی کوتاه به نقشه جهانی ویروس به راحتی آمار مبتلایان را در اختیار کارشناسان قرار میدهد. برای نمونه در چهارم مارچ ۲۰۲۰ تعداد مبتلایان در کشور اتریش صرفا ۲۹ نفر بوده است. پنج روز بعد این تعداد پنج برابر شده و به عدد ۱۵۷ رسیده است.
پروفسور فرانس وَیس بائر در دانشگاه وین از فرمولی ساده جهت یافتن مدل ریاضی تکثر ویروس استفاده کرده است.
N2=N1.2^x با قرار دادن دو عدد ۲۹ و ۱۵۷ به عنوان تعداد مبتلایان میتوان معادله را حل و برای دوره پنج روزه عدد x را معادل ۲٫۴۴ محاسبه و با تقسیم ساده تعداد روزها به شاخص فوق به «ضریب دوبرابر شدن ابتلا» دست پیدا کرد. که برای اتریش عدد ۲٫۱ روز خواهد بود.
این یعنی دو برابر شدن دانههای گندم در روی صفحه شطرنج پس از ۲٫۱ روز صورت میگیرد. در اینجا دانشمند اتریشی به عنوان کارشناس مشاور میکوشد با داشتن معادله ریاضی روند رشد مبتلایان را برای روزهای آینده محاسبه کند.
در این مسأله یکی دیگر از شاخصهای مهم و تعیینکننده، شناخت روند بیماری است. آمار چین نشان میدهد که ۸۱ درصد بیماران علائم خفیف دارند و قابل معالجه در منزل هستند. ۱۴ درصد داری شرایط مشکلتری هستند که نیاز به تخت بیمارستانی دارند و تنها ۵ درصد دچار بیماری وخیم هستند که نیاز به بستری در بخش مراقبتهای ویژه دارند. در مواجهه با بحرانی مثل کرونا، تعداد تختهای بیمارستان و از آن مهمتر تعداد تختهای بخش مراقبت ویژه اهمیت پیدا میکنند.
در کشور اتریش ۲۰۵۹ تخت مراقبت ویژه وجود دارد. جمعیت این کشور ۸/۸ میلیون است. بنابراین به ازای هر صدهزار نفر ۲۳٫۴ تخت مراقبت ویژه وجود دارد. البته باید توجه داشت که حدود نصف تختهای آی سی یو برای بیماران دیگری که به دلایل غیر از کرونا نیاز به مراقبتهای ویژه دارند معمولا پر شده است. اساسا نصف تختها خالی هستند که میتوان آنها را به بیماران مبتلا به کرونا اختصاص داد. این عدد برای کشور اتریش ۱۰۲۹ تخت در کل کشور میشود.
محاسبات آماری میتوانند نقطه گرهای شروع کمبود تختهای آی سی یو را پیشبینی کنند. اتریش در روز بیستم به این نقطه میرسد. یعنی در روز بیستم تعداد مبتلایان به کرونا که بیماری شدید دارند بیش از ظرفیت تختهای بخش مراقبتهای ویژه است و بیماران به امکانات درمانی دسترسی نخواهند داشت.
این یادداشت دسترسی به آمار تختهای آی سی یو در کشور ایران ندارد. هدف این میزگرد و این یادداشت این است که مسوولان وزارت بهداشت که به آمار دقیق این تختها دسترسی دارند، برنامهریزیهای کلان خود را بر اساس تعداد تختهای ICU انجام بدهند.
کاهش روابط اجتماعی
تصمیمهایی چون کاهش ارتباطهای اجتماعی با هدف کاهش شاخص ضریب ابتلا یکی از مهمترین اقدامات در جهت کنترل بیماری است. ممکن است تصور شود این بیماری در بیشتر موارد خفیف است و کاهش موارد ابتلا مساله خیلی مهمی نیست؛ در حالیکه اگر بتوان تعداد موارد ابتلا را نصف کرد، به دنبال آن تعداد مواردی که در طیف ۵ درصد وخیم بیماری هستند هم نصف میشود و در واقع آمار مرگ و میر به نصف کاهش خواهد یافت.

بنابراین هر کدام از ما با ماندن در خانه و کاهش روابط اجتماعی بیش از آنکه فکر میکنیم در کاهش مرگ و میر سهیم میشویم.
اقداماتی همچون بستن مدارس، کنسل کردن بازیهای ورزشی یا ایجاد منع رفت آمد و همچنین قرنطینه کردن مناطق آلوده مهمترین روشها در کنترل بیماری هستند.
نکته اپیدمیولوژیکی که وجود دارد این است که اگر دو سوم افراد جامعه به این ویروس آلوده شوند اپیدمی «خود به خود» برطرف میشود. بنابراین حتی اگر قرنطینه در کاهش موارد ابتلا نقش خیلی زیادی نداشته باشد، مهمترین هنر آن کاهش است.
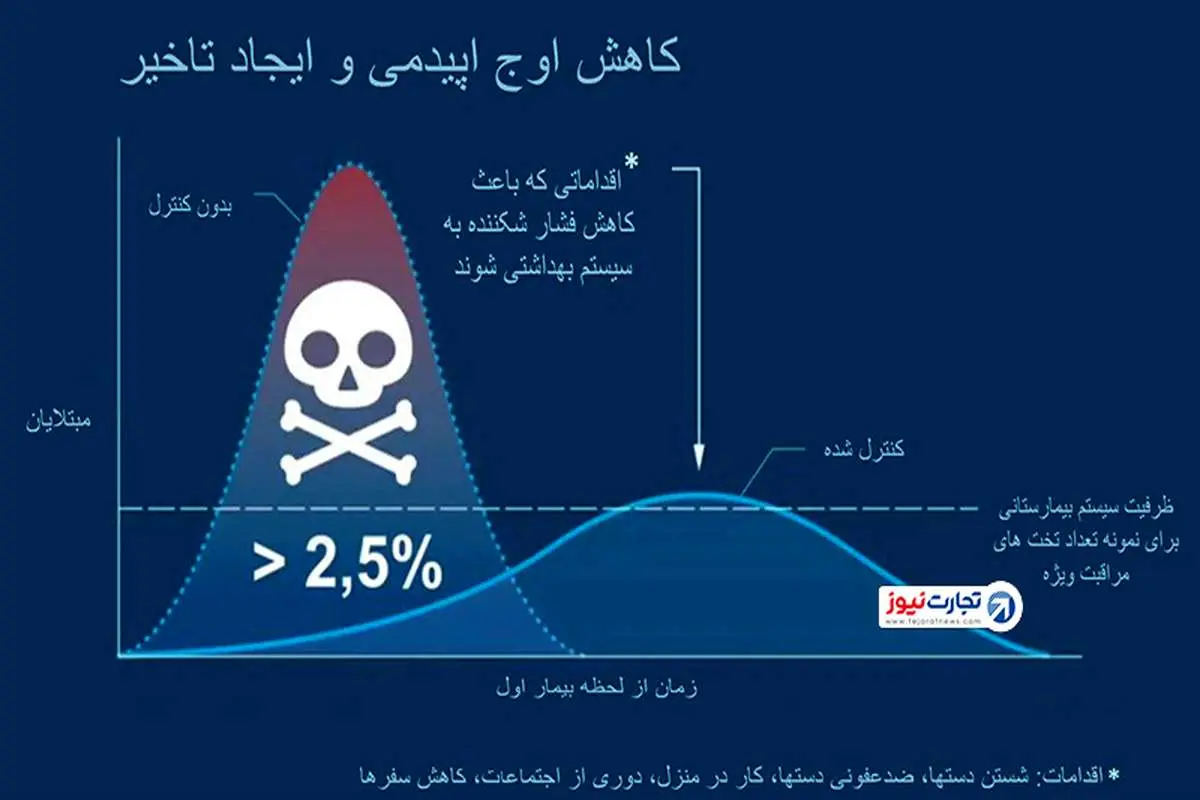
شیب نمودار ابتلا در یک بازه زمانی بیشتر است. در نتیجه تعداد موارد ابتلا در یک بازه زمانی کوتاه به پیک خود نمیرسد که فراتر از ظرفیت تختهای آی سی یو باشد.
سرعت ابتلا باید در حدی تنظیم شود که تختهای آی سی یو کفاف آن ۵ درصد موارد وخیم و کشنده را بدهد.
دکتر فرانس ویس بائر میکوشد تا در مدل ریاضی خود و با توجه به دادههای بالا، ضریب فوق را به حدی پایین بیاورد که اوج نمودار از تعداد تختهای مراقبت ویژه فزونی نگیرد. او هر چند میداند که توان کاهش تعداد بیماران را ندارد و به بیان دیگر مساحت زیر هر دو نمودار برابر هستند ولی میتواند از تعداد مرگ و میر این اپیدمی بکاهد، هرچند زمان درگیری بیماری در جامعه خود را افزایش میدهد.
در اینجا علم ریاضی است که جان انسانها را نجات میدهد. تعیین عدد دقیق شاخص رشد ویروس، تعداد تختهای ICU و مدلهای ریاضی اطلاعات ارزشمندی را در اختیار مدیریت بحران قرار میدهد. به بیان دیگر مدیران بحران لازم است بدانند مدت زمان لازم برای ویروس جهت حرکت از یک خانه به خانه دیگر صفحه شطرنج خود و رشد دو برابری چقدر است. کلیدی که میتواند نجات دهنده جان افراد باشد. نیم نگاهی به آمار دوبرابر شده ایتالیا صرفاً طی ۴ روز (۱۵ مارچ ۲۱ هزار مبتلا و ۱۴۴۰ فوتی در مقابل چهار روز پیش از آن با ۱۰ هزار بیمار و ۶۳۰ فوتی) کافی است تا اهمیت مساله و لزوم واکنش سریع دولتمردان را دریابیم. بدیهی است اگر رشد تصاعدی ویروس در طی سه روز باشد و جلسات مدیریت بحران هفتهای یک مرتبه برگزار شوند، آنگاه از این نشست تا آن نشست تعداد اجساد ۴ برابر شدهاند.
توضیح: این یادداشت حاصل همفکری سه کارشناس در حوزههای مختلف است. حافظ باجغلی، روانپزشک و رواندرمانگر؛ فرزاد باجغلی، دکترای اقتصاد مهندسی و مدیر عامل یک شرکت خصوصی کامپیوتر در وین و شهرام اختری، کارشناس عمران و مدرس ریاضی.














نظرات